UNIVERSIDAD TÉCNICA DE MACHALA
FACULTAD DE INGENIERÍA CIVIL
PRIMERO "C"
GROUP 2
RESPONSABLES:
JHONNY E. AJILA SÀNCHEZ
LUIS E. ROBLES ERAZO
BYRON A. FERNÀNDEZ CHAMBA
MICHAEL J. PRADO MACIAS
TUTOR:
ING. FREDDY JUMBO
MODULO
NUEVAS TECNOLOGÍAS DE LA COMUNICACIÓN E INFORMACIÓN
2014 - 2015
INTRODUCCIÓN
El Cálculo
diferencial es una de las herramientas fundamentales para la Ingeniería,
aplicándola a la misma para diseños de suma importancia para el desarrollo de
la vida.
Es
fundamental recordar la aplicación del cálculo para tal fin de disponer de
conocimientos y datos a aplicarse para que este Proyecto permita, de la manera más
clara, entender cómo influyen las derivadas en la aplicación a las
construcciones de categoría Civil.
Se
realizaran cálculos para resolver problemas como el desfogue de aguas lluvias
de una ciudad hasta la creación de grandes estructuras. Sin embargo para todas
estas grandes obras civiles debemos analizar una a una las técnicas del cálculo
utilizaremos para realizar nuestro propósito mediante el estudio y sus impacto que generaría nuestra investigación en las obras civiles.
Objetivo General
El curso permitirá al alumno introducirse a:
·el estudio de las funciones, sus
gráficas, comportamiento, propiedades y aplicaciones;
·la apropiación de los
procedimientos y técnicas del cálculo diferencial y
·la aplicación de estos
procedimientos y técnicas a la solución de problemas muy diversos, favoreciendo
el uso y la integración de los conocimientos adquiridos en aritmética, álgebra,
geometría, trigonometría y geometría analítica
y, al mismo tiempo, propiciará en el alumno
·el desarrollo de sus habilidades
para el análisis, el razonamiento y la comunicación de su pensamiento, a través
de la solución de problemas que le permitan percibir e interpretar su entorno
espacial desde la perspectiva del Cálculo y, a su vez, faciliten en el futuro
la asimilación de aprendizajes más complejos y la resolución de problemas en el
área tecnológica.
Observación General
El orden de los contenidos en cada tema no
implica una secuencia de enseñanza, sino que el profesor podrá modificarlo como
considere conveniente para el desarrollo de su curso y el aprendizaje de sus
alumnos.
Aquellos contenidos que no aparezcan
explícitamente citados en los programas y que el profesor quiera introducir
para enriquecer su curso, podrán ser tratados a través de ejercicios, problemas
y aplicaciones, dentro de los tiempos marcados por cada unidad.
Lineamientos Generales
Durante todo el desarrollo del curso, se
promoverán el análisis, la solución y la discusión de problemas en clase, en un
ambiente que favorezca en los alumnos la apreciación de su propio trabajo
personal, el de sus compañeros y el de su profesor.
Deberá tenerse presente que la solución de
problemas es la que permite generar conocimiento, favorece su asimilación y
ayuda a distinguir lo esencial de lo menos importante. En este proceso el
profesor es un facilitador del aprendizaje, que problematiza, proporciona
información y crea códigos de instrucción, al mismo tiempo que organiza el
trabajo en clase de manera que sus alumnos puedan resolver los problemas planteados
y avanzar hacia nuevos conocimientos, a lo largo de la actividad, es importante
que los alumnos desarrollen su capacidad para comunicar su pensamiento y se
acostumbren gradualmente a los diversos medios de expresión matemática:
lenguajes natural, simbólico y gráfico, así como el uso de tablas y diagramas.
Las tres líneas indispensables a desarrollar en el curso de
Cálculo Diferencial
Este programa de Cálculo Diferencial contempla
tres grandes líneas de desarrollo, que se deberán ir tratando y desplegando a
lo largo de todo el curso:
·El conocimiento de las funciones,
sus gráficas, comportamiento, propiedades y aplicaciones.
·La apropiación gradual de los
procedimientos y técnicas del Cálculo Diferencial.
·La aplicación de los procedimientos
del Cálculo Diferencial a la solución de problemas diversos.
Es importante hacer notar que no es
conveniente que haya largos períodos dedicados exclusivamente a la ejercitación
de las fórmulas y reglas de derivación, sino que, a medida que los estudiantes
hayan aprendido nuevos procedimientos para derivar, los utilicen en la solución
de problemas y aplicaciones.
El programa deberá cumplirse hasta sus últimas
unidades, pues éstas preparan a los alumnos para el siguiente curso, donde se
estudiarán las técnicas de integración. Lo anterior será posible si el profesor
distingue siempre lo esencial de lo accesorio y no insiste en la ejercitación
excesiva de temas de poca importancia para los cuales bastará resolver uno o
dos ejemplos en el salón de clase y dejar otros como tarea. También deberán
evitarse aquellos tratamientos teóricos superfluos o innecesarios, o tratar de
agotar un tema desde el principio pues el programa ha sido diseñado de tal
manera que los conocimientos esenciales puedan utilizarse a lo largo de todo el
curso.

CALCULO DIFERENCIAL
Unidad 1. Funciones y Límites
Objetivo. Que
el estudiante amplíe y enriquezca gradualmente sus conocimientos sobre la
noción de función como la expresión de una cantidad en términos de otra; que
desarrolle las habilidades para resolver problemas que le lleven a plantear
funciones y a darles solución por medio de tablas de valores o de gráficas,
mediante el análisis e interpretación de las relaciones que se establecen entre
las variables. Que, a partir del análisis del comportamiento local y para
valores muy grandes de la variable independiente, trace gráficas de funciones y
describa los comportamientos utilizando la notación de límites.
1.1 Revisión de la noción de función, enfatizando:
-
La idea de función como la
expresión de una cantidad en términos de otra;
-
Los problemas que llevan a
plantear funciones; su solución por medio de una tabla de valores o de una
gráfica;
-
Los ejemplos para revisar las
nociones de variable independiente y variable dependiente, y de dominio y rango
de una función.
1.2 Ejercicios de trazado de gráficas, análisis local y para valores muy
grandes de x del comportamiento de una función e introducción de la notación de
límites para indicar los comportamientos observados, en particular:
-
De funciones racionales alrededor
de los ceros del denominador, con ejemplos que ilustren los casos en que pueden
presentarse: síntomas y discontinuidades removibles.
-
De polinomios y funciones
racionales para valores muy grandes de x (positivos y negativos).
Unidad 2. La derivada y sus interpretaciones
Objetivo. Que
el estudiante identifique las propiedades de la derivada a partir de sus
interpretaciones física y geométrica. Que emplee la definición en el cálculo de
derivadas sencillas y aplique éstas en la solución de problemas de razón de
cambio, cálculo de tangentes y aproximación de funciones.
2.1 La derivada y sus interpretaciones física y geométrica:
-
Como rapidez o razón de cambio instantánea
de una función, con ejemplos extraídos de la física, la economía, la biología y
otras disciplinas.
-
Como pendiente de la recta
tangente a la gráfica de la función en un punto.
-
La tangente como la recta que
mejor aproxima a la función en un punto; observación sobre una gráfica de las
relaciones entre la inclinación de la tangente y el crecimiento de la función.
2.2 Cálculo de derivadas sencillas utilizando la definición, por ejemplo,
2.3 Aplicaciones elementales de la derivada: cálculo de tangentes y
normales; de razones de cambio; primeros cálculos aproximados utilizando la
fórmula:
carpetas que contiene los archivos necesarios:
Unidad 3. Derivadas de funciones algebraicas
Objetivo. Que
el estudiante conozca y se ejercite en el uso de las fórmulas y las reglas de
derivación de las funciones algebraicas, así como en la aplicación de la regla
de la cadena para derivar funciones algebraicas tanto explícitas como
implícitas.
3.1 Primeras fórmulas y reglas de derivación:
-
Derivadas de (constante); y polinomios.
-
Derivadas de una función por una
constante, de la suma, la resta, el producto y el cociente de dos funciones.
-
La regla de la cadena y sus
aplicaciones para derivar funciones algebraicas, en particular de las
funciones:
Unidad 4. Aplicaciones de la derivada.
Objetivo. Que
el estudiante amplíe y enriquezca sus conocimientos de la derivada por medio de
las aplicaciones de las derivadas sucesivas de una función, el estudio de los
puntos críticos de una función, las relaciones entre los signos de la primera y
la segunda derivadas y las características de la función, y el trazado de
gráficas en la solución de problemas muy diversos.
4.1 Aplicaciones de la primera derivada a la solución de problemas muy
diversos de rapidez de cambio.
4.2 Derivadas sucesivas, significado físico de la segunda derivada,
ecuación de movimiento uniformemente acelerado.
4.3 Relaciones entre el signo de la 1ª y 2ª derivadas y el carácter
creciente o decreciente y el sentido de la concavidad de la gráfica de una
función, en particular, criterios de la 1ª y 2ª derivadas para máximos y
mínimos. Aplicaciones a:
-
La solución de problemas de máximos
y mínimos.
-
El trazado de gráficas y el
estudio de los puntos críticos de una función (construcción de la tabla de
variación de una función).
Unidad 5. Funciones exponenciales
Objetivo. Que
el estudiante amplíe y enriquezca sus conocimientos de la función exponencial,
su gráfica, comportamiento, propiedades y aplicaciones, como modelo de
distintas situaciones. Que emplee la derivada de la función exponencial para
profundizar su estudio y ampliar sus aplicaciones.
5.1 La función exponencial general:
5.2 La función y sus aplicaciones
como modelo de distintas situaciones (crecimiento poblacional, decaimiento
radiactivo, interés compuesto continuo, etc.).
5.3 Conocimiento de la derivada de y ejercicios muy
diversos de aplicación de la fórmula:
al
cálculo de derivadas, en particular, derivadas sucesivas de .
Unidad 6. Funciones circulares
Objetivo. Que
el estudiante amplíe y enriquezca sus conocimientos de las funciones
circulares, sus gráficas, comportamientos, propiedades y aplicaciones como
modelos de distintas situaciones. Que emplee las derivadas de las funciones
circulares para profundizar su estudio y ampliar sus aplicaciones.
6.1 Revisión del círculo trigonométrico; conocimiento de las gráficas de
las funciones circulares y su comportamiento. Gráficas de funciones de las
formas
6.2 Movimiento armónico simple, ejemplos ilustrativos (oscilación de un
resorte, péndulo simple, pistón oscilante,...).
6.3 Derivada de las funciones sen(x) y cos(x); discusión de los límites:
6.4 Deducción de las derivadas y aplicaciones al
cálculo de las derivadas de las fórmulas.
6.5 Aplicaciones al estudio de: las relaciones entre, por ejemplo, las funciones
y sus derivadas
sucesivas; las gráficas y los puntos críticos de funciones circulares; al
cálculo de razones de cambio y; a la resolución de problemas de máximos y
mínimos.
Unidad 7. Diferenciales y cálculos aproximados
Objetivo. Que
el estudiante explore la noción de diferencial como la mejor aproximación
lineal de una función y la aplique en el cálculo de incrementos y la estimación
de errores, para resolver problemas muy diversos.
7.1
Cálculo
aproximado de raíces: método de Newton.
7.2 La tangente como la mejor aproximación lineal de la función alrededor
de un punto. Cálculo aproximado de valores de una función mediante la fórmula:
7.3 Ejemplos para introducir la noción de diferencial de una función;
aplicaciones de la diferencial para calcular aproximadamente el incremento de
una función y para estimar errores.
Unidad 8. Funciones inversas: derivadas del logaritmo y las
funciones circulares inversas (10 horas)
Objetivo. Que
el estudiante, a partir del estudio de las funciones inversas y sus derivadas,
particularmente las inversas de las funciones exponencial y circulares, revise
la noción de función como una regla de correspondencia entre dos conjuntos de
valores.
carpetas que contiene los archivos necesarios:
Bibliografía
Hughes-Hallet, D. et al.
|
Cálculo
|
CECSA
|
1995, México, DF
|
Larson, et al.
|
Cálculo Diferencial e Integral
|
Mc Graw-Hill
|
6ª Ed. 1999, México, DF
|
Purcell, Edwin J.
|
Cálculo Diferencial e Integral
|
Prentice-Hall
|
6ª Ed. 1992, México, DF
|
Abreu, José Luis,
et al.
|
Cálculo
Diferencial e Integral (6 volúmenes)
|
LIMUSA
|
1ª Ed. 1983, México, DF
|
Cruse-Lehman
|
Lecciones de Cálculo
(2 volúmenes)
|
Fondo Educativo Interamericano
|
1972, México
|
Edwards, C.H.
y Penney, D.E.
|
Cálculo
|
Prentice-Hall
|
1987, México
|
Stewart, James
|
Cálculo
|
Thomson
|
1999, México, DF
|
Mochón, Simón
|
Quiero entender el cálculo
|
Iberoamérica
|
1ª Ed. 1995, México, DF
|
Swokoski, Earl W.
|
Cálculo con Geometría Analítica
|
Iberoamérica
|
|
Zill, Dennis G.
|
Cálculo con Geometría Analítica
|
Iberoamérica
|
1995, México, DF
|
Hockett, Shirley O.
y Sternstein, Martin
|
Cálculo por objetivos y aplicaciones
|
CECSA
|
1ª Ed. 1982, México, DF
|
Ayres, Frank.
|
Cálculo Diferencial e Integral
|
Mc Graw-Hill
|
3ª Ed. 1991, México, DF
|
Anfossi, A.
|
Cálculo Diferencial e Integral
|
Progreso
|
México, DF
|
Del Grande, Duff
|
Introducción al Cálculo Elementos
|
HARLA
|
4ª Ed. 1982, México, DF
|
Leithold
|
Cálculo con Geometría Analítica
|
HARLA
|
4ª Ed. 1982, México, DF
|
Protter, Murray H.
|
Cálculo con Geometría Analítica
|
Fondo Educativo Interamericano
|
3ª Ed. 1980, México DF
|
Rangel, Luz Maria
|
Funciones y Relaciones
|
ANUIES; Trillas
|
1ª Ed. 1975, México, DF
|
REGLAS DE LA DERIVACIÓN BÁSICAS
REGLAS DE LA CADENA
REGLAS DERIVACIÓN LOGARITMICAS
PROYECTO DE CALCULO DIFERENCIAL APLICADA A LA INGENIERÍA CIVIL

UNIVERSIDAD
TÉCNICA DE MACHALA
UNIDAD EDUCATIVA DE INGENIERIA CIVIL
PROYECTO INTEGRADOR
DE SABERES
TITULO:
Cálculo Diferencial Aplicada a la Ingeniería Civil
TEMA:
Aplicación de la derivada en el diseño de un túnel de
forma elíptica para la construcción de un alcantarillado pluvial.
INTEGRANTES:
Jhonny Elvis Ajila Sánchez
Luis Edwin Robles Erazo
Byron Alexander Fernández Chamba
María Fernanda Toledo García
RESPONSABLE:
Mgs. Ing Civil. Ginger Andrea Carrión Rugel
AÑO LECTIVO
2014-2015
DATOS INFORMATIVOS
·
Aplicación de la
derivada en el diseño de un Túnel de forma elíptica para la construcción de un
alcantarillado pluvial.
·
Jhonny Elvis Ajila Sánchez
·
Luis Edwin Robles Erazo
·
Byron Alexander Fernández Chamba
·
María Fernanda Toledo García
UNIVERSIDAD TECNICA DE MACHALA
El Cálculo
diferencial es una de las herramientas fundamentales para la Ingeniería,
aplicándola a la misma para diseños de suma importancia para el desarrollo de
la vida. Citemos (HOWARD, 1991) .
Es
fundamental recordar la aplicación del cálculo para tal fin de disponer de
conocimientos y datos a aplicarse para que este Proyecto permita, de la manera más
clara, entender cómo influyen las derivadas en la aplicación a las
construcciones de categoría Civil.
Se
realizaran cálculos para resolver problemas como el desfogue de aguas lluvias
de una ciudad hasta la creación de grandes estructuras. Sin embargo para todas
estas grandes obras civiles debemos analizar una a una las técnicas del cálculo
utilizaremos para realizar nuestro propósito mediante el estudio y sus impactos
que generaría nuestra investigación en las obras civiles.
3.1 DESCRIPCION DEL PROBLEMA
Evaluar por medio de
la aplicación del cálculo a las construcciones de túneles de forma elípticas
que se construyen para el alcantarillado pluvial de un sector residencial, y
calcular la pendiente necesaria que se debe aplicarle para que la obra este es
óptimas condiciones para su uso.
3.2 PROBLEMA GENERAL Y SECUNDARIOS
Empleando las
técnicas de cálculo, derivación Implícitas y la geometría analítica, que
utilizamos para obtener la pendiente necesaria para tener un flujo hidráulico
en el alcantarillado pluvial para mejorar el desfogue de aguas lluvias de una
ciudad.
3.3 OBJETIVO GENERAL
Aplicando técnicas de geometría y Derivación Implícitas,
para obtener la información necesaria para la Creación de un sistema de
alcantarillado pluvial en base a túneles
elípticos que eliminen el exceso de aguas lluvias de una ciudad.
·
Considerando la aplicación de la derivada
implícita en la construcción de una
elipse para hallar la pendiente necesaria para
túnel en un punto específico a partir de una ecuación geométrica
analítica de sus dimensiones.
·
Estimar las técnicas aplicadas al túnel
elíptico para diseñar nuevas redes de alcantarillado pluvial más eficientes.
·
Representar el problema a resolver por medio
de las Derivadas implícitas para darle una solución eficaz a la creación de
túneles para construcciones sanitarias.
·
Identificar el cálculo de la derivada
aplicada en la construcción y de un túnel elíptico.
·
Realizar una comparación de la ecuación
obtenida a partir de la geometría del túnel elíptico para desarrollar su
pendiendo por medio de las derivadas Implícitas y darle un mejor calculo al
proyecto a ejecutarse.
¿Cómo interpretar el
cálculo diferencial de unos sistemas de alcantarillado de tipo pluvial, de
forma elíptica aplicando las derivadas implícitas a las ecuaciones?
La
interpretación del cálculo aplicada para este proceso, es la derivada Implícita
en la ecuación de la elipse, lo cual nos lleva a determinar la pendiente en su
punto dado para su construcción respectiva en una obra civil.
La
Ingeniería civil es una de las carreras técnicas más aplicadas en la vida
cotidiana, considerándola técnica por sus conocimientos de física, química, cálculo,
gestiones ambientales e hidráulicas, geológicas vías y de transporte. La
ingeniería es una las ramas más importantes y es por tanto que se debe tener
una corresponsabilidad con el medio ambiente y de muy alto compromiso con la
humanidad en su desarrollo.
Las
aplicaciones de la ingeniería globalizan otras carreras, que son de gran
utilidad para ejercer la labor de un ingeniero, emprendiendo en el diseño y los
estudios a realizar, comprendiendo los pro y contra que se pueden presentar a
la hora de realizar proyectos de grandes escalas; tales como vías primarias,
aeropuertos, saneamiento y diseño
urbanístico, con el fin de no causar un gran impacto al medio ambiente y
aplicando tecnologías que beneficien tanto la naturaleza, como el bien
ciudadano.
Tengamos
en cuenta, que la ingeniería no solo abarca la física y/o matemáticas, el cálculo
diferencial es una herramienta esencial para
proceder con la formulación y obtención de los valores que necesitamos
para desarrollar óptimamente un trabajo; ya sea desde el cálculo de un área de
una casa rectangular, hasta calcular la pendiente de un sistema de
alcantarillado para desfogar las aguas de una ciudad para evitar catástrofes
por inundaciones.
Aplicando
a continuación los métodos fundamentales del cálculo para obtener la pendiente
de un sistema de alcantarillado pluvial, partimos desde este punto principal
para realizar un proyecto de sistemas sanitarios y explicaremos las técnicas
aplicadas a continuación,
poner cita bibliográfica.
La
Geometría Analítica es una parte de la Matemática que establece una conexión
entre la Geometría Euclidiana y el Algebra. Según (ANFOSSI, 1949)
Estudia
las figuras geométricas utilizando un sistema de coordenadas y resuelve los
problemas geométricos por métodos algebraicos, las coordenadas (x, y) se
representan por grupos numéricos y las figuras por ecuaciones. ANEXO3
La
distancia entre dos puntos se calcula por medio de la siguiente formula:
Muchos fenómenos
físicos implican cantidades variables-la velocidad de un cohete, la devaluación
de la moneda por la inflación, el número de bacterias de un cultivo, la
intensidad de un movimiento telúrico, el voltaje de una señal eléctrica, etc.
Se desarrollarán las herramientas matemáticas para expresar con precisión las
razones o tasas de cambio. Supóngase que P(Xo,Yo) y Q(X1,Y1) son puntos de la
gráfica de la función f. Entonces la recta secante que une PyQ tiene la
pendiente.
Definición de derivada.- La derivada de una función  es otra función
es otra función  (lease “f
prima”) cuyo valor en cualquier numero x
es
(lease “f
prima”) cuyo valor en cualquier numero x
es
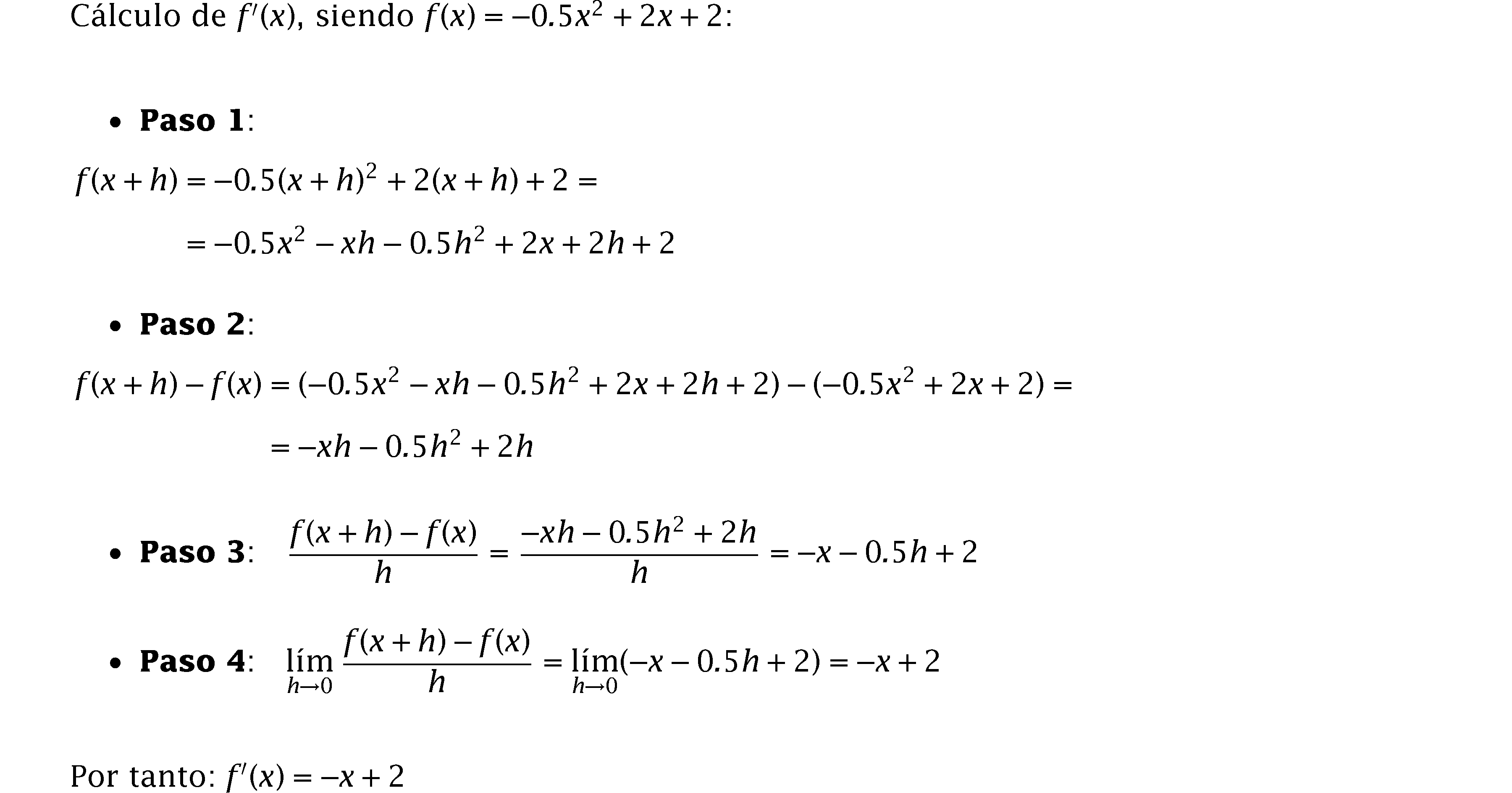
Si este
límite existe, decimos que es derivable en x. Determinar una derivada recibe el nombre de derivación; la parte
del cálculo asociada se denomina calculo diferencial. ANEXO4
La
derivada implícita determina una fórmula para , que es válida para toda
función derivable  tal que este definida implícitamente por una ecuación
dada.
tal que este definida implícitamente por una ecuación
dada.
El
proceso de las derivadas implícitas se da únicamente en las ecuaciones que
especifican una función.
El
método para calcular una función implícita consiste en derivar los dos miembros
de relación y este procedimiento se lo conoce como derivación implícita. Cítese
(PURCELL, 2007)
·
Ejemplo de explicación: Derivación
implícita.- Igualamos las derivadas de los dos lados. Después de utilizar la
regla para el producto en el primer término, obtenemos,
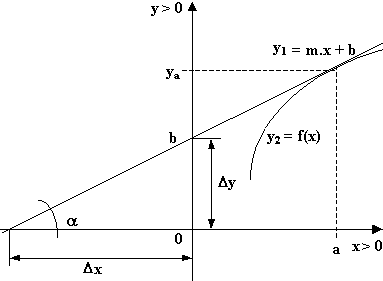
Después
de utilizar la regla para el producto en el primer término, obtenemos,
5. MARCO METODOLÓGICO
5.1 METODOLOGIA APLICADA AL PROYECTO
1.
Métodos
científicos y/o técnicas de cálculo utilizadas.
La aplicación de
geometría y calculo diferencial (derivadas implícitas).
En el desarrollo del
ejercicio geométrico de la elipse, en el que vamos a fundamentar nuestros
conocimientos aplicando el cálculo de las derivadas Implícitas, primeramente
aplicando pre-calculo en la obtención de la formula geométrica para el área de la elipse y obtener la
ecuación a la que vamos aplicarle el cálculo de la pendiente para el correcto
diseño de un sistema de alcantarillado Pluvial.
Fundamentaremos los
conocimientos obtenidos en cálculo
diferencial poniendo en práctica en el campo de la ingeniería civil.
Métodos
y recursos aplicados para la sustentación del proyecto
1.
Validaremos primeramente nuestro
proyecto con la deducción geométrica del túnel, desarrollando las ecuaciones
para obtener la primera ecuación en la cual nos fundamentaremos para el cálculo
diferencial. ANEXO Analizando paso a paso las técnicas aplicadas
al ejercicio.
2.
A continuación aplicaremos el cálculo
diferencial a nuestra ecuación obtenida en base al pre-calculo, tomando en
cuenta la explicación de la misma en el transcurso del planteo del ejercicio.
3.
Consideraremos las herramientas
necesarias para aplicar todas las ecuaciones necesarias para nuestro proyecto
este correctamente sustentado y desarrollado en la construcción civil.
1.
Procedimiento
a.
Buscar el problema en la ingeniería
civil en un sistema de alcantarillado Pluvial, para aplicarle cálculo
diferencial y demostrar la aplicación en su diseño.
b.
Seguidamente aplicamos geometría al
elemento que se construirá en el alcantarillado pluvial que se dará de forma
elíptica.
c.
Encontramos la ecuación a partir de la aplicación de la geometría analítica
del ejercicio que vamos a desarrollar y aplicarle Cálculo diferencial.
d.
Después interpretamos y aplicamos las
derivadas implícitas a las ecuaciones obtenidas, para obtener la pendiente en
un punto dado para el Sistema pluvial.
e.
Evidenciar que el resultado obtenido por las técnicas
aplicadas sea satisfactorio para el diseño del sistema y tenga sus respectivas
conclusiones y recomendaciones necesarias para su entendimiento.
2.
Obtención
de la primera ecuación en base a su geometría
Aplicaciones:
Geotecnia.
Se
ha diseñado un túnel de forma elíptica. El centro se encuentra a 10 metros de
la superficie. La altura mayor de la elipse es de 10 m y la menor es de 6
metros.
Figura 2
Encuentre
la ecuación de dicha elipse, tenga en cuenta que la altura estará en términos
de profundidad, por ende, el eje vertical será positivo hacia abajo.ANEXO2
Solución:
Centro:
(0,10)
Radio
mayor: 5 m
Radio
menor: 3m
Ecuación
de la elipse:
Derivadas implícitas.
Aplicaciones:
Geotecnia[1].
En
el ejercicio anterior, de la elipse cuya ecuación es la siguiente:
Se
requiere calcular la pendiente para hallar el estado de esfuerzos en dicho
planos. Calcular la pendiente para un punto dado.
Solución:
·
El propósito de la investigación
y análisis del mismo nos lleva la correcta utilización de las técnicas que aplicaremos
en la Ingeniería civil para la construcción de obras que desarrollaremos, para
nuestro propio porvenir. El cálculo de la pendiente de un túnel elíptico para
el desfogue de aguas pluviales (aguas lluvias), es de enorme importancia, así
como proyectos a partir de ecuaciones obtenidas geométricamente. Poniendo en
conocimiento todas las técnicas aprendidas en el desarrollo de pendientes con
el fin de darle un uso beneficios a nuestros conocimientos para desarrollar
proyectos de suma importancia y profundizarlos más en creación de nuevas
técnicas para obtener el fin esperado.
·
En base a los resultados
ejecutados en el proyecto contaremos con la información necesaria que nos
permitirá predecir los flujos que tendremos en nuestra red de alcantarillado, con
el logro que se propuso aplicar en obtención y facilitación de su construcción.
Recomendaciones
para el uso de la derivada y la facilidad de cálculo en la geotecnia de un
túnel.
·
Recomendamos investigar
acerca de geometría analítica ya que es un tema fundamental en cálculo
diferencial.
·
Requerir ayuda del tutor ya
que es de mucha importancia para guiarnos en el proyecto para tener una idea
más clara del tema a plantear.
·
Conocer los conceptos a
utilizarse en el proyecto en este caso
las derivadas implícitas para llevar a cabo un trabajo bien realizado.
·
Elaborar graficas de los
ejercicios propuestos en el tema para así tener una visión más clara y
detallada, permitiéndonos así elegir el camino correcto.
·
Es esencial en
obras públicas el diseño de una red exclusiva para el desalojo de aguas
residuales, planteando el cálculo correcto que se debe ejecutar en la
construcción de la red, tal como se contempla en planos y especificadores
técnicas basadas en nuestras en Cálculo Diferencial (Derivadas Implícitas).
·
De suma
importancia el cálculo para aplicarse en cada tramo a construirse el
alcantarillado, para saber la pendiente y sus velocidades, para evitar la
obstrucción en el sistema de alcantarillado.
·
Deben respetarse
los valores obtenidos por la geometría de la elipse, para partir con la primera
ecuación a la cual le aplicaremos su pendiente respectiva con los conocimientos
de derivadas implícitas, para realizar una evaluación tanto constructiva y como
en el cómputo de sus datos para determinar la factibilidad en el sistema a
diseñarse.
·
Se deberá
verificar que tanto los datos aplicados (geometría y derivación) sean
correctamente aplicados para evitar problemas de funcionamiento.
·
PURCELL,
E.; RIGDON, S Y VARBERG, D. (2007). Cálculo
diferencial e integral (9na Ed.)... Capítulo II:”Derivada”,
“Derivadas Implícitas” Págs.100, 130. Washington: Pearson Education. ISBN 10:
970-26-0989-5
·
GRAMVILLE, A. (2009). Calculo diferencial e integral. Capítulo VI: “Derivadas implícitas”.
Pág. 90. México: Limusa.
·
HOWARD, Antón. (1991). Cálculo y
Geometría Analítica (Tomo I). Capitulo III. “Derivación”, “Derivadas
Implícitas”. Pags.147, 147-148.Editorial Limusa: México. ISBN 968-18-1538-6.
·
ANFOSSÍ, A. (1949). Geometría Analítica. (Décimo Tercera Edición).Capitulo
IV. “La Elipse”.Pág.81. Editorial Progreso, S.A: México.
·
CHARLES, Lehmann. (1980). Geometría Analítica. Capitulo VII. “La Elipse”.
Pag.173-190.Editorial Limusa: México. ISBN 968-18-1176-3.
·
KINDLE, Joseph. (1984). Geometría Analítica: Plana y del Espacio. (Octava
impresión). Capítulo VI. “La Elipse”. Pag.51-58.Editora Xalco S.A: México.
·
LARSSON, HOSTETLER, Robert, Roland. “Calculo y geometría analítica”.
Capítulo 2, La derivada. Sexta Edición. Volumen 1. Editorial Mac Graw hill
Medellín-Colombia. disponible en pdf link:
http://archive.org/details/CalculoVol.1LarsonHostetler. Recuperado el 14 de
julio del 2014. Capítulo 2 pag, 106-110. ISBN:
Los
números que se utilizan en el álgebra son los números reales. Hay un número
real en cada punto de la recta numérica. Los números reales se dividen en
números racionales, números irracionales y números enteros los cuales a su vez
se dividen en números negativos, números positivos y cero (0) .Podemos verlo en
esta tabla:
Un
número real es racional si se puede
representar como cociente a/b, donde a sea un entero y b
sea un entero no igual a cero. Los números racionales pueden escribirse en
forma decimal.
Existen dos maneras:
Existen dos maneras:
* Decimales terminales
* Decimales que se repiten
infinitamente
Los
números reales que no pueden ser expresados en la forma a/b, donde a
y b son enteros se llaman números irracionales. Los números irracionales no tienen decimales
terminales ni decimales que se repiten infinitamente.
Recta Numérica
Definición: La recta real o recta numérica es un
sistema de coordenadas en donde los números reales pueden representarse.
Para construir una recta
numérica, primero se escoge un punto en la recta que será un punto
arbitrario al que le llamaremos cero (0). Este punto es llamado el origen de la
recta numérica. El origen separa la recta en dos partes, el lado positivo y el
lado negativo. A la derecha del origen está el lado positivo y el negativo está
a la izquierda. En el lado derecho van números enteros positivos (en orden
sucesivo) y en el lado izquierdo se escriben los números enteros negativos (en
orden sucesivo), estos se marcan en unidades equidistantes.
ORDEN
DE LOS NÚMEROS REALES
Es
importante recordar que para cualesquiera dos números reales diferentes a los
que llamaremos a y b, siempre uno es mayor que el otro.
|
Notación
|
Definición
|
Terminología
|
|
a > b
a < b
|
a – b es positivo
a – b es negativo
|
a es mayor que b
a es menor que b
|
La distancia de un
número en la recta numérica desde cero (0) se llama valor
absoluto. Se representa con el símbolo |x| . El valor absoluto de un
número se calcula de la siguiente manera:
·
si
el número es negativo, lo convertimos a positivo.
·
si
el número es cero o positivo, se queda igual.
Ejemplos:
|7| = 7
|-7|
= 7
Definición:
|
Valor Absoluto
|
Sea x un número real, representaremos su
valor absoluto como |x| léase “valor absoluto de x” y lo definimos como:
-x si x < 0
|x| =
x si x ≥ 0
|
“Es decir, el valor absoluto de un número negativo (x
< 0) es su simétrico; o sea, un número con la misma magnitud, pero positivo.
En cambio, cuando el número es positivo, su valor absoluto coincide con él; lo
mismo ocurre para cero, su valor absoluto es él mismo”.
Por
ejemplo: |-23| =23
Pero también,
|23| = 23
Operaciones con valor absoluto
Sean a y b números reales y
sea n un entero positivo.
1.  2.
2.


3.  4.
4.

Propiedades de Valor Absoluto
Sean a y b
números reales y sea k un número real positivo:
- -│a│≤
a ≤│a│
- │a│≤
k si y sólo si –k ≤ a ≤ k
- k ≤│a│
si y sólo si k ≤
a ó
a ≤ -k
- Desigualdad
triangular: │a+b│ ≤ │a │ + │ b│
Las propiedades 2 y 3 también
son válidas si se sustituye ≤ por <.
Propiedades de las Desigualdades
Sean a, b, c, d y k números reales.
|
Propiedad Transitiva
Suma de Desigualdades
Suma de una Constante
Producto por una
constante
positiva
Producto por una
constante
negativa
|
Desigualdades Lineales
Una inecuación o desigualdad lineal es lo mismo que
una ecuación lineal pero cambiando el signo de igualdad por signo(s) de
desigualdad.
Los signos de
desigualdad . Para resolver una desigualdad lineal se utilizan los
mismos pasos que se usan para resolver una ecuación lineal. Como ejemplo, vamos
a resolver las siguientes desigualdades:
Ejemplo 1) Resolver: 3 > x - 8.
Sumando la misma
cantidad a ambos lados:
3 > x - 8
3 + 8 > x - 8 + 8
11 > x
x < 11
El conjunto solución es: (-∞, 11).
Ejemplo
2) Resolver: 2x-5 < 7
Solución:
2x-5
< 7 desigualdad
original
2x-5+5
< 7+5 sumar 5 a ambos miembros
2x < 12 simplificar
½ (2x) < ½ (12) multiplicar a ambos miembros por ½
x < 6 simplificar
El
conjunto solución es: (-∞, 6).
Una regla
importante en las desigualdades es que cuando se divide por un número negativo,
el signo de desigualdad cambia.
Ejemplo
4) Resolver: -3 ≤ 2-5x ≤ 12
Solución:
-3
≤ 2-5x ≤ 12
Desigualdad original
-3-2
≤ 2-5x-2 ≤ 12-2
restar 2
-5 ≤ -5x ≤ 10
Simplificar
- (1/5) (-5) ≥ - (1/5) (-5x) ≥ - (1/5)
(10) Multiplicar a ambos miembros por
–(1/5) e invertir ambas .
desigualdades.
1 ≥ x ≥ -2 Simplificar
El
conjunto solución es [-2,1].
Desigualdades Cuadráticas
Ejemplo 7) Resolver: x2
< x+6
Solución:
x2 < x + 6
Desigualdad original
x2 - x - 6 < 0 Escribir en
forma usual
(x – 3)(x + 2) < 0 Factorizar
El polinomio x2
- x - 6 tiene los ceros x = -2 y x = 3, por tanto tiene los intervalos prueba
(-∞,-2),(-2,3) y (3,∞).
La solución de la desigualdad original es (-2, 3).
WEBGRAFIA:
·
HNANDEZ; ELSIE. Calculo diferencial e integral.
“Aplicacione de la derivada. 2013 . Recuperado el 20 de agosto del 2014.
Disponible en Pdf en Link: http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesderivada/html/node4.html
·
SOTO, HERNANDEZ.
Efrain, Elsie Calculo
diferencial . “Aplicacione de la derivada”. ”.3.2 “Valores máximos y minimos de
una función”. Pag 192 y 193. Febrero 2013 . Recuperado el 20 de agosto del
2014. Disponible en Pdf en Link: http://www.aprendematematicas.org.mx/notas/calcdiferencial.html
BIBLIOGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Sexta
Edición, Volumen 1,mac Graw hill editorial Medellín-Colombia, disponible en pdf
link: http://archive.org/details/CalculoVol.1LarsonHostetler
, recuperado el 17 de julio del 2014. Capítulo 2 pag, 119-122.
·
GRANVILLE, William Anthony, Calculo diferencial2.
Calculo Integral, Editorial Limusa S.A de CV, sexta edición,
ISBN-13:978-968-18-1178-5, Mexico, disponible en pdf, recuperado el 17 de julio
2014 , Pag 37 – 43.
ANEXO 1:
Definición de elipse
Una
elipse es una curva cerrada que es simétrica sobre sus ejes verticales y
horizontales. La distancia entre puntos antipodales en la elipse, o pares de
puntos cuyo punto central está en el centro de la elipse es máxima a lo largo
del eje principal o
diámetro transversal y un mínimo a lo largo del eje menor perpendicular o
diámetro conjugado.
Formulas:
Elipse
Área = π R1 R2
Elipse
perímetro = 2π (√ (R12
+ R22) / 2)
Volumen
del elipsoide = (4π/3) R1 R2
R3
Donde
R1
es un radio mayor
R2
es un radio mayor
ANEXO 2:
ANEXO 3:
ANEXO 4:
Reglas de derivación
Derivadas
inmediatas: Sean a, b y k constantes (números reales) y consideremos a “u” y “v” como funciones.
Derivada
de una constante
|
|
Función
identidad
|
|
Derivada
de la función afín
|
|
Derivada
de una potencia
|
|
Derivada
de una raíz cuadrada
|
 Nota:
se deduce de la regla para derivar potencias. Nota:
se deduce de la regla para derivar potencias. |
Derivada
de una raíz cualesquiera
|
 Nota:
se deduce de la regla para derivar potencias. Nota:
se deduce de la regla para derivar potencias. |
Derivada
del seno
|
|
Derivada
del coseno
|
Derivadas
de sumas, productos, cocientes y funciones compuestas.
Derivada
de una suma/resta
|
|
Derivada
de una constante por una función
|
|
Derivada
de un producto
|
|
Derivada
de un cociente
|
|
Regla
de la cadena
|
[1]
Parte de la geología que estudia la composición y propiedades de la superficie
terrestre para asentamientos y construcciones públicas.
REFERENCIAS BIBLIOGRÁFICAS
HEMISEMESTRE
WEBGRAFIA:
·
ANALITICA,
Vitutor. “Analitica en vectores, vectores en el espacio”. 2008. Recuperado el
2014. Disponible en:http://www.vitutor.com/analitica/vectores/vectores_espacio.html
·
ANALITICA,
Vitutor. “Analitica en vectores, vectores en el espacio”. 2008. Recuperado el
2014. Disponible en http://www.slideshare.net/figuerona/espacio-tridimensional.
BIBLIOGRAFIA:
·
ESPOL RECURSOS,
Leonardo Barmontec. Actualización13 mayo
2012.CALCULO DIFERENCIAL, RECURSOS: Límites con funciones trigonométricas
ejemplos y definición, Recuperado 18 de junio 2014. No hay página Disponible en: http://blog.espol.edu.ec/inpol/2014/04/11/limites-trigonometricos-resueltos/
BIBLIOGRAFIA:
·
HERNANDEZ S,
Elsie. Actualización febrero 2013. CALCULO DIFERENCIAL E INTEGRAL CON
APLICACIONES, Recuperado 07 de junio 2014. Disponible en: http://www.tec-digital.itcr.ac.cr/revistamatematica/Libros/Calculo_Diferencial_Integral/CALCULO_D_I_ELSIE.pdf
Referencias:
Ø http://www.biografiasyvidas.com/biografia/n/newton.htm
BIBLIOGRAFIA:
·
ÁLGEBRA LINEAL
APLICADA, Noble Ben y Daniel James W. Prentice-HallHispanoamerica
S.A. Tercera Edición. México, 1989.
·
CARREÑO, Ximena Campos y Ximena Cruz
Schmidt. algebra. Publicaciones
Cultural, Primera Edición, 2003.
BIBLIOGRAFIA:
·
ÁLGEBRA LINEAL
APLICADA, Noble Ben y Daniel James W. Prentice-HallHispanoamerica
S.A. Tercera Edición. México, 1989.
BIBLIOGRAFIA:
·
ESPOL RECURSOS,
Leonardo Barmontec. Actualización13 mayo
2012.CALCULO DIFERENCIAL, RECURSOS: Límites con funciones trigonométricas
ejemplos y definición, Recuperado 18 de junio 2014. No hay página Disponible en: http://blog.espol.edu.ec/inpol/2014/04/11/limites-trigonometricos-resueltos/
BIMESTRE
BIBLIOGRAFIA:
·
GRANVILLE,
LONGLEY, William, Raymond. “Calculo Integral y
diferencial”. Capitulo III derivación. Sexta Edición. Volumen 1. Mac Graw hill
editorial Medellín-Colombia. disponible en pdf link: http://archive.org/details/CalculoVol.1LarsonHostetler.
Recuperado el 14 de julio del 2014. Capítulo 2 pag, 25-29. ISBN:
13-978-968-18-1178-5.
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”.
Capítulo 2, La derivada. Sexta Edición. Volumen 1. Editorial Mac Graw hill
Medellín-Colombia. disponible en pdf link: http://archive.org/details/CalculoVol.1LarsonHostetler.
Recuperado el 14 de julio del 2014. Capítulo 2 pag, 106-110. ISBN:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Capítulo 2 pag107. Sexta
Edición. Volumen 1. Editorial mac Graw hill . Medellín-Colombia. disponible en
pdf link: http://archive.org/details/CalculoVol.1LarsonHostetler.
Recuperado el 14 de julio del 2014.
BIBLIOGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Capítulo
2: Derivada. Sexta Edición. Volumen 1. Capítulo 2 pag 112- 115. Editorial
mac Graw hill.Medellín-Colombia.
disponible en pdf link: http://archive.org/details/CalculoVol.1LarsonHostetler,
recuperado el 14 de julio del 2014.
BIBLIOGRAFIA:
·
ÁLGEBRA LINEAL
APLICADA, Noble Ben y Daniel James W.
Prentice-HallHispanoamerica S.A. Tercera Edición. México, 1989.
·
CARREÑO, Ximena Campos y Ximena Cruz
Schmidt. algebra. Publicaciones
Cultural, Primera Edición, 2003.
WEBGRAFIA:
·
HNANDEZ; ELSIE. Calculo diferencial e integral.
“Aplicacione de la derivada. 2013 . Recuperado el 20 de agosto del 2014.
Disponible en Pdf en Link: http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesderivada/html/node4.html
·
SOTO, HERNANDEZ.
Efrain, Elsie Calculo
diferencial . “Aplicacione de la derivada”. ”.3.2 “Valores máximos y minimos de
una función”. Pag 192 y 193. Febrero 2013 . Recuperado el 20 de agosto del
2014. Disponible en Pdf en Link: http://www.aprendematematicas.org.mx/notas/calcdiferencial.html
BIBLIOGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Sexta
Edición, Volumen 1,mac Graw hill editorial Medellín-Colombia, disponible en pdf
link: http://archive.org/details/CalculoVol.1LarsonHostetler
, recuperado el 17 de julio del 2014. Capítulo 2 pag, 119-122.
·
GRANVILLE, William Anthony, Calculo diferencial2.
Calculo Integral, Editorial Limusa S.A de CV, sexta edición,
ISBN-13:978-968-18-1178-5, Mexico, disponible en pdf, recuperado el 17 de julio
2014 , Pag 37 – 43.
BIBLIOGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Sexta
Edición1999, Volumen 1,mac Graw hill editorial Medellín-Colombia, disponible en
pdf link: http://archive.org/details/CalculoVol.1LarsonHostetler
, recuperado el 17 de julio del 2014. Capítulo 2 pag, 118-126.
·
STEWART, James, Calculo diferencial, Editorial
Publish or perish, quinta edición 2002,
ISBN-13:978-968-18-1178-5978-0-534-39339-7, disponible en pdf, recuperado 17 de
julio 2014, pag 50- 55.
BIBLIOGRAFIA:
·
GRANVILLE,
LONGLEY, William, Raymond. “Calculo Integral y
diferencial”. Capitulo IV derivación “reglas para derivar funciones
algebraicas” Sexta Edición. Volumen 1. Mac Graw hill editorial Medellín-Colombia.
disponible en pdf link: http://archive.org/details/CalculoVol.1LarsonHostetler.
Recuperado el 30 de julio del 2014. Capítulo 2 pag, 36-42. ISBN:
13-978-968-18-1178-5.
WEBGRAFIA:
·
TORRE, Alba. “derivadas de las funciones
trascendetales. Recuperado 30 de julio 2014.
En línea .disponible en: http://es.slideshare.net/ftorrealba/derivadas-de-las-funciones-trascendentes.
BIBLIOGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Capítulo 2. 2.4 “la regla de la cadena. pag130-136. Sexta Edición. Volumen 1. Editorial mac Graw hill.
Medellín-Colombia. disponible en pdf link:
http://archive.org/details/CalculoVol.1LarsonHostetler.
Recuperado el 30 de julio del 2014.
BIBLIOGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Capítulo
2: Derivada. Octava Edición. Volumen 1. Capítulo 3. pag 172- 173. Editorial
mac Graw hill.Medellín-Colombia.
disponible en pdf link:
http://www.cobaehtolcayuca.com/LECTURAS/Calculo%20Larsson%208%20edicion.pdf,
recuperado el 30 de julio del 2014.
BIBLIOGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Capítulo
2: Derivada. Octava Edición. Volumen 1. Capítulo 3. pag 173- 175. Editorial
mac Graw hill.Medellín-Colombia.
disponible en pdf link:
http://www.cobaehtolcayuca.com/LECTURAS/Calculo%20Larsson%208%20edicion.pdf,
recuperado el 30 de julio del 2014.
BIBLIOGRAFIA y WEBGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Capítulo
2: Derivada. Octava Edición. Volumen 1. Capítulo 3. pag 173- 175. Editorial
mac Graw hill.Medellín-Colombia.
disponible en pdf link:
http://www.cobaehtolcayuca.com/LECTURAS/Calculo%20Larsson%208%20edicion.pdf,
recuperado el 30 de julio del 2014.
·
GORDILLO, Juan.disponible en
pdf.rescatado el 30 de julio 2014. Link:.
http://www.juangordillo.com/derivadas/derivadas4.html
BIBLIOGRAFIA y WEBGRAFIA:
·
LARSSON,
HOSTETLER, Robert, Roland. “Calculo y geometría analítica”. Capítulo
2: Derivada. Octava Edición. Volumen 1. Capítulo 3. pag 173- 175. Editorial
mac Graw hill.Medellín-Colombia.
disponible en pdf link:
http://www.cobaehtolcayuca.com/LECTURAS/Calculo%20Larsson%208%20edicion.pdf,
recuperado el 30 de julio del 2014.
·
GORDILLO, Juan.disponible en
pdf.rescatado el 30 de julio 2014. Link:.
http://www.juangordillo.com/derivadas/derivadas4.html
BIBLIOGRAFIA :
·
GRANVILLE,
LONGLEY, William, Raymond. “Calculo Integral y
diferencial”. Capitulo VI. “Derivadas sucesivas de una funcion” Sexta Edición.
Volumen 1. Mac Graw hill editorial Medellín-Colombia. disponible en pdf link: http://archive.org/details/CalculoVol.1LarsonHostetler.
Recuperado el 04 de Agosto del 2014. Capítulo 2 pag, 93-94. ISBN:
13-978-968-18-1178-5.
·
DIAZ, Jl .disponible en
pdf.rescatado el 04 de Agosto 2014. Link:. http://www.mat.uson.mx/~jldiaz/Documents/Derivadas/.
BIBLIOGRAFIA y WEBGRAFIA:
·
GRANVILLE,
LONGLEY, William, Raymond. “Calculo Integral y
diferencial”. Capitulo IV. Derivacion. “reglas para derivar funciones
algebraicas. Funciones implicitas” Sexta Edición. Volumen 1. Mac Graw hill
editorial Medellín-Colombia. disponible en pdf link: http://archive.org/details/CalculoVol.1LarsonHostetler.
Recuperado el 04 de Agosto del 2014. Capítulo 2 pag, 49,50. ISBN:
13-978-968-18-1178-5.
·
DIAZ, Jl .disponible en
pdf.rescatado el 04 de Agosto 2014. Link:. http://www.tec-digital.itcr.ac.cr/revistamatematica/cursos-linea/CALCULODIFERENCIAL/curso-elsie/derivadafuncion/html/node19.html









No hay comentarios.:
Publicar un comentario